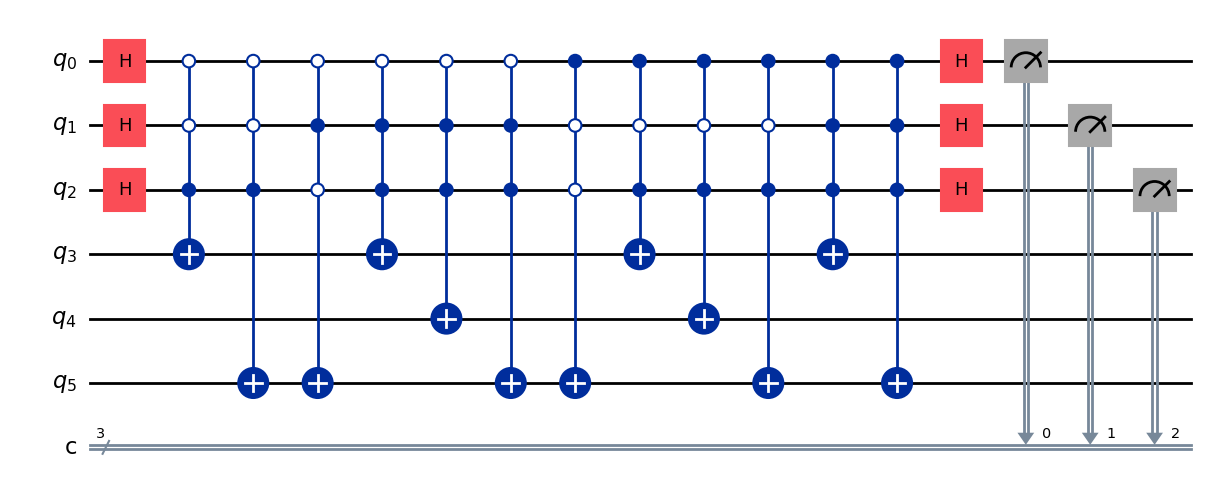
David P. DiVincenzo's Criteria
Who is David DiVincenzo? What criteria did he outline for quantum computers? And how hard is it for computers to abide by it?
The Quantum Computer was first proposed by mathematician Yuri Manin in 1980 alongside Richard Feynman in 1982 in the hopes that it would describe the quantum phenomena occurring in nature without apparent reason. However, for many years the question was left hanging: How would we go about building such a machine? If you ever hear someone ask: “Oh, how well does this quantum computer follow DiVincenzo’s criteria?”, then you can be sure that this person has quite a holistic view of quantum computers. The reason being, even though quantum computers vary hugely on design principles, operations and many other facets, they should ultimately align with these foundational rules in order to be a useful quantum computer. Again, even the term useful may differ depending on which source you consult - but nowadays the quantum computing industry refers to DiVincenzo whenever the debate arises.
David DiVincenzo
Born in 1959, David is an American theoretical physicist, specialising in quantum information research and quantum information processing. Having previously attended Cornell University and University of Pennsylvania; he is now a professor at the Institute for Quantum Information at RWTH Aachen University. One of David’s most popular papers outlines 5 essential requirements any quantum computer should adhere to - these are now known as the DiVincenzo criteria. Although such rules were set in 1996 and were reportedly aimed at the level of ‘kindergarten children’, their beautiful simplicity allows them to act of leading guidelines in current computer builds today. Before we dive into them, a few important things should be addressed:
One of the most important fields, Quantum Computer Benchmarking, is significantly aided by the DiVincenzo criteria. The criteria can act as a framework to compare the viability of different quantum computational methods.
Although the framework has had such a positive impact, it doesn’t quite cover all aspects of quantum computation today, e.g. Error Correction or Distributed Modular approaches.
Nevertheless, it is certain that the David’s criteria will remain a landmark in the history of the development of Quantum Computers. Thanks David!

Criteria 1: A Quantum Computer must be scalable with a ‘well-behaved’ qubit
If you recall the previous article about the qubit, you will remember that the general structure of a qubit is like a ladder with two rungs. We have a lower rung and a higher rung with an energy gap between the two - and we can use this property for quantum computation. Regardless of what physical system we choose, a ‘well-behaved’ qubit will stay in-between these two levels. If energy transitions can easily occur above these levels, then this is a badly behaved qubit (although note that higher level qubits, known as qudits, are sometimes intentional).
The main issue quantum computers face is that whilst it is relatively easy to create a well-behaved physical qubit, it remains difficult to scale them. This effectively means that placing them side by side and maintaining complete control of all qubits is a hard problem. We require exponentially larger setups for quantum computers with more qubits - negating the benefit we get from faster computation against classical computers. A good way of picturing the issue of scaling is as follows:
Imagine you are tasked with keeping one cup of water level on a tray. This would be an easy task and you would surely remain in control of the water cup. Now, what if instead you are tasked with keeping 100 cups of water level on a tray - you would find that even the smallest movement would cause a huge spillage. This is the analogy for the difficulty of scaling.
Nevertheless, there are certain ways of navigating and managing the scaling issue. Most importantly, if we do manage to create a quantum computer that can scale with ease it will open the doorway to fully functional and useful quantum computing.
Criteria 2: We need a starting reference state
When we do quantum computation, we have to start from an initial state each time. Therefore, it is important that we generally have a simple initial state that we can put our qubits into before computation. Having a reliable starting point means that we can trust our algorithms and know that they provide reliable and reproduceable results. Further, many quantum algorithms require certain initialisation setups in order to perform correctly, such as Quantum Phase Estimation. DiVincenzo believed it was important to have a clean and reliable starting point for computation as this ensured consistent results and ease in reproducing any setup. Today we find that the ability to consistently initialise our qubits to the ‘ground state’ - lowest rung of the ladder - is crucial for quantum error correction.
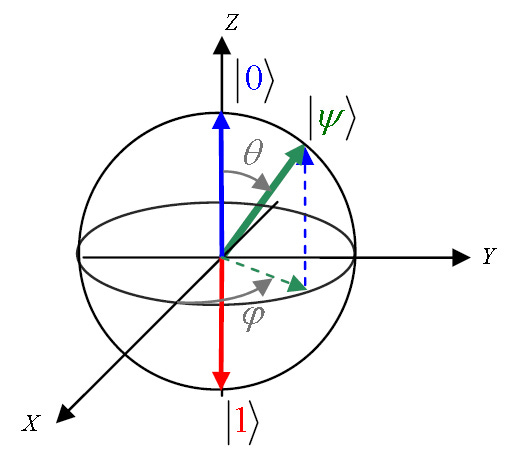
Criteria 3: Relatively long coherence times
Coherence is a measure of how quantum a state is, it can be maximally quantum or minimally quantum (also known as just a classical state). Quantum decoherence is primarily due to the inevitable external environment that exists outside of the quantum computer. As particles infiltrate the quantum computer, unwanted effects occur and the systems loses its quantumness. Whilst I could just quote time frames, what is most important is not the time that a quantum state remains coherent for, but rather the time it remains coherent relative to the speed of operations on the quantum computer. Even if a qubit only lasts for a short amount of time, if we are able to run lots of operations using it within this time then there’s no problem.
If a system suffers from decoherence it means that the quantum circuits will decohere before finishing a computation. This limits how complex we can make our quantum circuits as well as the complexity of the algorithms we can run. This is why I previously mentioned that photons make for amazing qubits - they rarely decohere.
Criteria 4: A universal set of quantum gates
The quantum gate can be thought of a set of instructions or an operation that is performed on a quantum computer. For example, a quantum gate might ask the qubit to switch from state 0 to state 1. It might also put the qubit into a superposition of the two. Depending on many factors, such as the design of the computer or the natural decoherence that the qubits suffer from, a quantum computer will have a set of quantum gates that it is able to run. These are the ‘native’ gates that the computer is designed to be able to perform.
A universal set of quantum gates is a set of gates that can perform any type of transformation on a quantum computer to create any type of algorithm or desired circuit. This set should only contain the basic 1-qubit or 2-qubit gates as we only need them in order to perform any arbitrary desired function. Although we have yet to discuss quantum gates, here is an example of a universal gate set:
{Hadamard Gate (H), Phase Gate (S), π/8 gate (T), CNOT gate}
With these 4 gates you are able to perform any possible function you desire on a quantum computer. If you only had, say, the Hadamard gate then you would be limited to being able to represent only a handful of states.
Criteria 5: The ability to measure
Measurement is the foundation of all quantum algorithms, circuits and of all computation. If we cannot measure the result of our quantum process then indeed all of quantum computation is a fruitless exercise! Usually we measure many many times, sometimes exceeding 100,000 times, and we plot the results to see which result occurred most frequently. This is the golden standard of quantum measurement.
Criteria 5 and 1/2: Measuring specific qubits
This is actually part of criteria 5 but I’m separating it to emphasise that the ability to measure specific qubits is incredibly important - as set out by DiVincenzo. The ability to measure individual qubits without disturbing the rest of the quantum system allows one to retain the overall quantumness. This is important as many quantum algorithms, such as IQPE, require targeted and repeated measurements of just one qubit at various stages. This is also very physically challenging as this requires the ability to isolate and control just one qubit at a time.
Some extra ideas from DiVincenzo
For quantum communication there should be the ability to convert between stationary and flying qubits.
Stationary qubits, as per the name, are physically permanent qubits that stay in the same place and are built into the computer. Flying qubits ‘fly’ around and can be things such as photons that contain the quantum information within. The ability to convert, when necessary, between these two modes of information is key to allowing for third-party communication between quantum computers. Such notions lead us into the development of the quantum internet and of modular distributed quantum computing.
For quantum communication there should be the ability to transmit flying qubits between locations.
This is the second hurdle we face. Even when we are able to transfer quantum information from being stored on a physical qubit to a photon, as the photon travels it suffers from signal attenuation. This means that the strength of all the photons diminish with distance and become ‘lost’ (leaving the desired path). Furthermore, as robust as photons are, they still suffer from decoherence so even if they make it to the other side they might not correctly convey the quantum information they were intended to. If you ask me, sending quantum photons through optical fibres is our best and most cost-effective shot. They already exist and work well for our current internet; with a few tweaks we may create successful and wide-scale communication between quantum computers.
Final comments
It is a solid method to respect criteria within the field of Quantum computing. The reason I believe this is that every time there is a newfound ‘breakthrough’ it is important to take it with a grain of salt. It is important to be critical and to question the information in front of you. If it indeed passes all checks, as we do with most physics, then let it become the current benchmark of innovation. Else let it serve as a reminder that physics is tough and as a recognition that physicists are out there working hard and looking for answers to unsolved questions. The DiVincenzo criteria serve as a manual for producing effective quantum computing. Indeed, adhering to each criterium requires a large amount of knowledge and hardware. Yet if you follow the recipe well enough you will be able to implement amazing quantum algorithms and demonstrate the naturally enhanced speed at which quantum computation can be performed!